Mastering the Karnaugh Map: A Complete Information to 4-Variable Simplification
Associated Articles: Mastering the Karnaugh Map: A Complete Information to 4-Variable Simplification
Introduction
With nice pleasure, we’ll discover the intriguing matter associated to Mastering the Karnaugh Map: A Complete Information to 4-Variable Simplification. Let’s weave fascinating data and provide contemporary views to the readers.
Desk of Content material
Mastering the Karnaugh Map: A Complete Information to 4-Variable Simplification
The Karnaugh map (Okay-map) is a strong graphical device utilized in Boolean algebra to simplify logical expressions. Whereas relevant to any variety of variables, its effectiveness is most pronounced with as much as 4 variables. Past 4 variables, the Okay-map’s visible readability diminishes, and different simplification methods grow to be extra sensible. This text delves deep into the intricacies of four-variable Okay-maps, offering a complete understanding of their development, utilization, and utility in digital logic design.
Understanding the Fundamentals: Boolean Algebra and Simplification
Earlier than diving into Okay-maps, it is essential to understand the underlying ideas of Boolean algebra. Boolean algebra offers with binary variables (0 and 1, representing false and true, respectively) and logical operations like AND (represented by ⋅ or just juxtaposition), OR (+), and NOT (′ or ¬). A Boolean expression describes a logical relationship between these variables. Simplification of Boolean expressions is paramount in digital circuit design, because it results in easier, more cost effective, and infrequently quicker circuits. Unsimplified expressions require extra logic gates, rising circuit complexity, energy consumption, and potential for errors.
The first objective of Okay-map simplification is to reduce the variety of phrases and literals in a Boolean expression. A literal is a single variable or its complement (e.g., A, A′, B, B′). Minimization reduces the {hardware} wanted to implement the logic perform, leading to a extra environment friendly and dependable design.
Establishing a 4-Variable Okay-Map
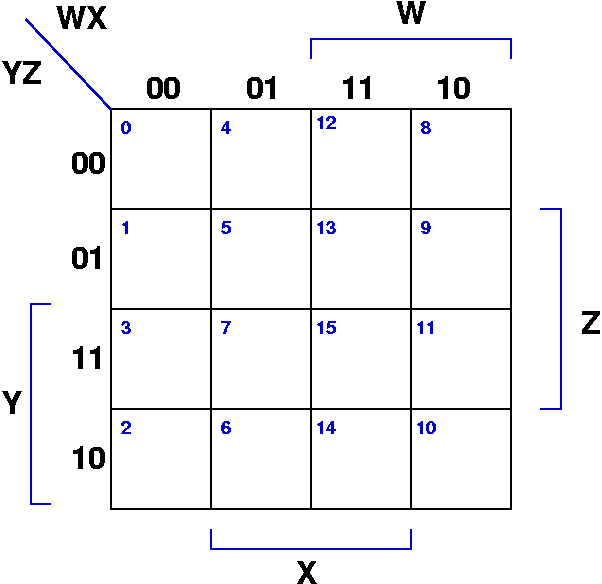
A four-variable Okay-map is a two-dimensional array representing all attainable mixtures of 4 enter variables. Usually, the variables are denoted as A, B, C, and D. The map is organized in a selected manner to make sure that adjoining cells differ by just one variable. This adjacency is essential for grouping phrases throughout simplification.
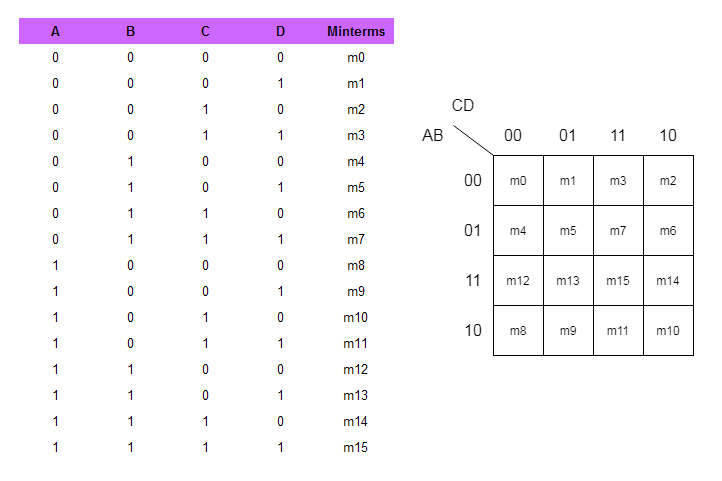
A 4-variable Okay-map is a 4×4 grid, as proven beneath:
CD
AB 00 01 11 10
00 m0 m1 m3 m2
01 m4 m5 m7 m6
11 m12 m13 m15 m14
10 m8 m9 m11 m10Every cell (m0 via m15) represents a minterm – a product time period the place every variable seems as soon as, both in its true or complemented type. As an example, cell m5 corresponds to the minterm A′BC′D. The association ensures that adjoining cells differ by just one variable. Notice the Grey code ordering of the variables alongside the axes, guaranteeing adjoining cells differ in just one bit. That is important for the simplification course of.
Populating the Okay-Map
The Okay-map is populated with the output values (0 or 1) of the Boolean perform for every minterm mixture of the enter variables. These values could be obtained from a fact desk, a Boolean expression, or a verbal description of the perform. A ‘1’ in a cell signifies that the corresponding minterm is current within the perform’s sum-of-products (SOP) type, whereas a ‘0’ signifies its absence.
Grouping Phrases for Simplification
The core of Okay-map simplification lies in grouping adjoining cells containing ‘1’s. These teams should be rectangular and comprise a lot of cells that may be a energy of two (1, 2, 4, 8, and many others.). Bigger teams result in easier expressions. The next guidelines govern grouping:
- Adjoining cells: Cells sharing a standard edge are thought of adjoining. Notice the wrap-around impact: the leftmost column is adjoining to the rightmost column, and the highest row is adjoining to the underside row.
- Group dimension: Teams should comprise 2n cells, the place n is an integer (1, 2, 4, 8, and many others.).
- Most grouping: Intention for the most important attainable teams to reduce the variety of phrases.
- Overlapping teams: Teams can overlap. A cell could be a part of a number of teams.
- All ‘1’s should be coated: Each cell containing a ‘1’ should be included in a minimum of one group.
Deriving the Simplified Expression
As soon as the optimum grouping is achieved, the simplified Boolean expression is derived by figuring out the variables that stay fixed inside every group. A variable that is still fixed in its true type (e.g., A) is included within the time period, whereas a variable that is still fixed in its complemented type (e.g., A′) can be included. Variables that change inside a bunch are eradicated.
For instance, a bunch of 4 adjoining cells may simplify to a time period with solely two variables. A bunch of eight cells may simplify to a time period with just one variable. The ultimate simplified expression is the sum (OR) of the phrases derived from every group.
Coping with Do not Care Situations
In some circumstances, sure enter mixtures could not happen or are irrelevant to the perform’s output. These are referred to as "do not care" situations and are represented by an ‘X’ within the Okay-map. Do not care situations could be strategically used to simplify the expression additional by together with them in teams of ‘1’s to create bigger teams.
Illustrative Instance: A 4-Variable Okay-Map Drawback
Let’s contemplate a Boolean perform with the next fact desk:
| A | B | C | D | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Populating the Okay-map with these values and grouping the ‘1’s optimally will end in a simplified expression. After grouping, we will derive the simplified Boolean expression. This course of requires cautious commentary and infrequently includes trial and error to seek out essentially the most environment friendly groupings. The ensuing simplified expression will signify the identical logic perform as the unique, however with fewer gates and improved effectivity.
Superior Methods and Concerns
Whereas the essential ideas are comparatively easy, mastering Okay-map simplification typically requires follow and a eager eye for optimum groupings. Superior methods contain contemplating completely different grouping methods and exploring potential trade-offs between the variety of phrases and literals.
Conclusion
The four-variable Karnaugh map is a strong device for simplifying Boolean expressions, resulting in environment friendly and cost-effective digital circuit designs. Understanding the ideas of Boolean algebra, the development and inhabitants of the Okay-map, and the foundations for grouping phrases are essential for profitable utility. Whereas seemingly easy, mastering Okay-map simplification requires follow and a radical understanding of the underlying ideas. With adequate follow, the Okay-map turns into a useful asset within the digital logic designer’s toolkit. Its visible nature supplies an intuitive strategy to Boolean simplification, making it a most popular methodology for a lot of engineers and college students alike. Nevertheless, it is essential to recollect its limitations for larger numbers of variables, necessitating the exploration of different minimization methods for extra advanced techniques.





Closure
Thus, we hope this text has supplied invaluable insights into Mastering the Karnaugh Map: A Complete Information to 4-Variable Simplification. We admire your consideration to our article. See you in our subsequent article!